<本文章转载自微信公众号：80后架构师，仅供学习参考，侵删>

轨道六根数是描述航天器轨道特性的基本参数，用于唯一确定航天器的轨道。在空间任务中，精确计算和描述轨道是任务设计和控制的核心部分。以下是对轨道六个要素的详细解释以及计算轨道位置和速度的具体实现。

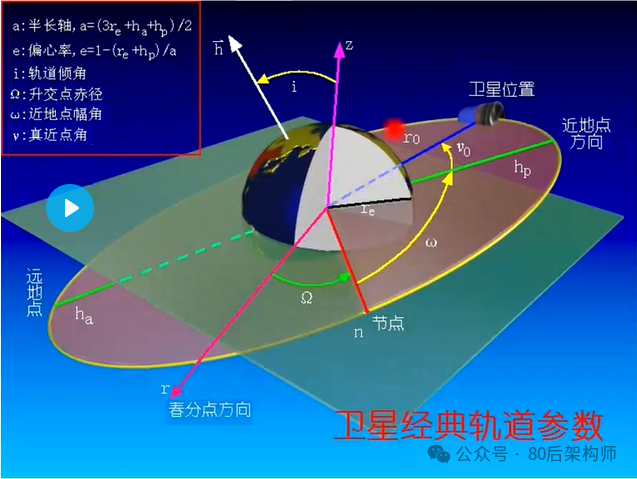
轨道六根数定义

1. 半长轴 (a)：

• 定义：轨道椭圆的长轴一半，决定了轨道的大小。
• 单位：通常为公里。
• 作用：轨道能量的指标，半长轴越大，轨道能量越高。

1. 偏心率 (e)：

• 定义：表示轨道的形状，是轨道椭圆度的量化指标。
• 范围：( 0 leq e < 1 )（椭圆轨道），( e = 0 ) 为圆轨道。
• 作用：影响航天器在轨道上的速度分布。

1. 倾角 (i)：

• 定义：轨道平面与参考平面（地球赤道平面）之间的夹角。
• 单位：弧度或度。
• 作用：决定轨道的倾斜程度，对卫星的覆盖区域有直接影响。

1. 升交点赤经 (Ω)：

• 定义：升交点（轨道从南向北穿过赤道的交点）相对于参考方向（通常是春分点）的角度。
• 单位：弧度或度。
• 作用：确定轨道在参考平面内的方向。

1. 近地点幅角 (ω)：

• 定义：从升交点到轨道近地点的角度。
• 单位：弧度或度。
• 作用：描述轨道椭圆的方向。

1. 平均近点角 (M)：

• 定义：在某一时刻，轨道上物体相对于近地点的角度。
• 单位：弧度。
• 作用：与时间相关，描述物体在轨道上的位置。

轨道状态计算

根据轨道六要素，可以通过开普勒方程和轨道力学计算航天器的位置和速度。以下是详细步骤：

1. 求解开普勒方程

开普勒方程：

[M = E - e cdot sin(E)]

其中：

• ( M ) 是平均近点角。
• ( E ) 是偏近点角（求解目标）。
• ( e ) 是偏心率。

求解方法：开普勒方程是非线性的，通常使用数值方法（如牛顿法）求解。

2. 计算径向距离

一旦求得 ( E )，可以计算径向距离 ( r )：

[r = a cdot (1 - e cdot cos(E))]

3. 计算轨道位置（极坐标）

航天器在轨道上的位置可以用极坐标表示：

• 角度 ( θ ) 是真近点角，可以通过以下公式计算：[tanleft(frac{θ}{2}right) = sqrt{frac{1+e}{1-e}} cdot tanleft(frac{E}{2}right)]
• 位置：
• ( r ) 为径向距离。
• ( θ ) 为极坐标的角度。

4. 转换到惯性坐标系

将极坐标转化为惯性坐标系（地心赤道惯性系）：

• 位置向量：[mathbf{r} = begin{bmatrix}r cdot (cos(Ω) cdot cos(ω+θ) - sin(Ω) cdot sin(ω+θ) cdot cos(i)) r cdot (sin(Ω) cdot cos(ω+θ) + cos(Ω) cdot sin(ω+θ) cdot cos(i)) r cdot (sin(i) cdot sin(ω+θ))end{bmatrix}]

Python实现

以下是一个完整的实现代码：

1. importmath
2. fromscipy.optimizeimportfsolve
3. importnumpyasnp
5. # 定义轨道元素
6. a=7000# 半长轴 (km)
7. e=0.01# 偏心率
8. i=math.radians(30)# 倾角 (rad)
9. Ω=math.radians(45)# 升交点赤经 (rad)
10. ω=math.radians(60)# 近地点幅角 (rad)
11. M=math.radians(20)# 平均近点角 (rad)
13. # 开普勒方程求解
14. defkepler_equation(E,M,e):
15. returnE-e*math.sin(E)-M
17. # 求解偏近点角E
18. E_guess=M# 初值
19. E_solution=fsolve(kepler_equation,E_guess,args=(M,e))[0]
21. # 计算径向距离r
22. r=a*(1-e*math.cos(E_solution))
24. # 计算真近点角θ
25. theta=2*math.atan2(
26. math.sqrt(1+e)*math.sin(E_solution/2),
27. math.sqrt(1-e)*math.cos(E_solution/2)
28. )
30. # 转换到惯性坐标系
31. x=r*(math.cos(Ω)*math.cos(ω+theta)-math.sin(Ω)*math.sin(ω+theta)*math.cos(i))
32. y=r*(math.sin(Ω)*math.cos(ω+theta)+math.cos(Ω)*math.sin(ω+theta)*math.cos(i))
33. z=r*(math.sin(i)*math.sin(ω+theta))
35. # 输出结果
36. print(f"轨道径向距离 r: {r:.2f} km")
37. print(f"真近点角 θ: {math.degrees(theta):.2f}°")
38. print(f"惯性坐标系位置向量: x = {x:.2f} km, y = {y:.2f} km, z = {z:.2f} km")

结果解释

1. 输入参数：轨道六要素由任务需求或观测数据提供。
2. 输出：

• 径向距离 ( r )：航天器离地球中心的距离。
• 真近点角 ( θ )：航天器在轨道上的位置。
• 惯性坐标系位置向量 ([x, y, z])：航天器在地心惯性坐标系的位置。

加入轨道速度计算

要计算航天器在轨道上的速度，我们需要使用轨道力学中的速度公式。根据轨道元素，航天器的速度可以通过以下几个步骤进行计算。

轨道速度计算

轨道上的速度分为两个部分：径向速度 和切向速度。总速度可以通过两者的矢量和计算得到。

1. 径向速度（Radial Velocity）

径向速度是指航天器沿着与轨道切线平行的方向（沿着轨道的径向）的速度。可以通过下面的公式来计算：

[v_r = frac{mu}{h} cdot e cdot sin(E)]

其中：

• ( mu = G cdot M{text{earth}} ) 是地球的标准引力参数，( G ) 为引力常数，( M{text{earth}} ) 为地球的质量。
• ( h ) 是轨道的角动量，计算公式为：[h = sqrt{a cdot (1 - e^2) cdot mu}]

2. 切向速度（Tangential Velocity）

切向速度是指航天器在轨道上的速度，与径向速度垂直，计算公式为：

[v_t = frac{h}{r}]

3. 总速度（Total Velocity）

总速度是径向速度和切向速度的矢量和。在开普勒轨道中，总速度的大小可以通过下列公式计算：

[v = sqrt{vr^2 + vt^2}]

Python实现：加入轨道速度计算

以下是加入轨道速度计算的完整代码：

1. importmath
2. fromscipy.optimizeimportfsolve
3. importnumpyasnp
5. # 定义轨道元素
6. a=7000# 半长轴 (km)
7. e=0.01# 偏心率
8. i=math.radians(30)# 倾角 (rad)
9. Ω=math.radians(45)# 升交点赤经 (rad)
10. ω=math.radians(60)# 近地点幅角 (rad)
11. M=math.radians(20)# 平均近点角 (rad)
13. # 地球的标准引力参数 (km^3/s^2)
14. mu=398600.4418
16. # 开普勒方程求解
17. defkepler_equation(E,M,e):
18. returnE-e*math.sin(E)-M
20. # 求解偏近点角E
21. E_guess=M# 初值
22. E_solution=fsolve(kepler_equation,E_guess,args=(M,e))[0]
24. # 计算径向距离r
25. r=a*(1-e*math.cos(E_solution))
27. # 计算轨道的角动量h
28. h=math.sqrt(a*(1-e**2)*mu)
30. # 计算真近点角θ
31. theta=2*math.atan2(
32. math.sqrt(1+e)*math.sin(E_solution/2),
33. math.sqrt(1-e)*math.cos(E_solution/2)
34. )
36. # 计算径向速度v_r
37. v_r=(mu/h)*e*math.sin(E_solution)
39. # 计算切向速度v_t
40. v_t=h/r
42. # 计算总速度v
43. v=math.sqrt(v_r**2+v_t**2)
45. # 转换到惯性坐标系
46. x=r*(math.cos(Ω)*math.cos(ω+theta)-math.sin(Ω)*math.sin(ω+theta)*math.cos(i))
47. y=r*(math.sin(Ω)*math.cos(ω+theta)+math.cos(Ω)*math.sin(ω+theta)*math.cos(i))
48. z=r*(math.sin(i)*math.sin(ω+theta))
50. # 输出结果
51. print(f"轨道径向距离 r: {r:.2f} km")
52. print(f"真近点角 θ: {math.degrees(theta):.2f}°")
53. print(f"惯性坐标系位置向量: x = {x:.2f} km, y = {y:.2f} km, z = {z:.2f} km")
54. print(f"径向速度 v_r: {v_r:.2f} km/s")
55. print(f"切向速度 v_t: {v_t:.2f} km/s")
56. print(f"总速度 v: {v:.2f} km/s")

代码说明

1. 径向速度 (vr) 和 切向速度 (vt) 被分别计算，并最终得到总速度 (v)。
2. 角动量 (h) 是通过轨道的半长轴和偏心率计算出来的，用于求解径向速度和切向速度。
3. 最终，输出包括：

• 位置向量：在惯性坐标系下的位置。
• 径向速度、切向速度 和 总速度：航天器在轨道上的速度。

结果示例

1. 轨道径向距离r:6562.68km
2. 真近点角θ:22.87°
3. 惯性坐标系位置向量:x=5844.37km,y=1984.68km,z=3304.82km
4. 径向速度v_r:0.73km/s
5. 切向速度v_t:7.74km/s
6. 总速度v:7.80km/s

总结

通过上述步骤，你可以计算出航天器在轨道上的位置和速度。轨道速度的计算对于航天器轨道控制、任务规划以及轨道保持至关重要。

<